Persistent Data Structures
September 8, 2006
Introduction and motivation
So far, we’ve seen only ephemeral data structures. Once changes have been made to an ephemeral data structure, no mechanism exists to revert to previous states. Persistent data structures are really data structures with archaeology.
Partial persistence lets you make modifications only to the present data structure but allows queries of any previous version. These previous versions might be accessed via a timestamp.
Full persistence lets you make queries and modifications to all previous versions of the data structure. With this type of persistence the versions don’t form a simple linear path — they form a version tree.
The obvious way to provide persistence is to make a copy of the data structure each time it is changed.
This has the drawback of requiring space and time proportional to the space occupied by the original data structure.
It turns out that we can achieve persistence with \(O(1)\) additional space and \(O(1)\) slowdown per operation for a broad class of data structures.
Applications
In addition to the obvious “look-back” applications, we can use persistent data structures to solve geometric problems by representing one of their dimensions as time.
Once example is the computational geometry problem of planar point location. Given a plane with various polygons or line segments which break the area up into a number of regions, in which region is a query point is located?
In one dimension, the linear point location problem can be solved with a splay tree or a binary tree, or even just a sorted array, that simply searches for the two objects on either side of the query point. So in one dimension, this problem can be solved in \(O(\log n)\) time.
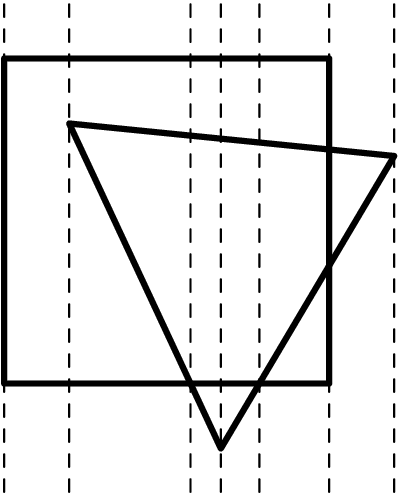
To solve the problem in two dimensions, break the plane into vertical slices at each vertex or point where lines cross. These slices are interesting because crossovers don’t happen inside slices: inside each slice, the dividing lines between regions appear in a fixed order, so the problem reduces to the linear case and requires a binary search (plus a bit of linear algebra). Figure 1 shows an example of how these slices look. To locate a point, first find the vertical slice it is in with a search on the point’s x coordinate, and then, within that slice, find the region it is in with a search on the point’s y coordinate (plus algebra). To do two binary searches takes only \(O(\log n)\) time, so we can locate a point in \(O(\log n)\) time. However, setting up the trees for searching a figure with \(n\) vertices will require \(n\) different trees, and each tree will take \(O(n\log n)\) time for sorting, so in total it takes \(O(n^2 \log n)\) time and \(O(n^2)\) space to do the preprocessing.
Suppose that the points in the input are in general position – that is no two have the same X or Y coordinate. Then between two adjacent slices of the picture, there can be at most one segment being removed and at most one segment being added. With points not in general position, we could either randomly perturb the input or allow slices of width 0. If we treat the horizontal direction as a timeline and use a persistent data structure, we can find the horizontal location of the point as a ‘version’ of the vertical point location data structure. So instead of thinking of the question as “in what two-dimensional region is the point \((x,y)\)?”, we can think of it as “at time \(t\), in what one-dimensional region is the point \(y\)?”. Every time we move to the next slab, we only have to insert or delete at most one region from a single persistent binary search tree. In this way, as long as we can keep the tree balanced, we can preserve the \(O(\log n)\) query time and use only \(O(n\log n)\) preprocessing time and \(O(n)\) space.
Making pointer-based data structures persistent
Now let’s talk about how to make arbitrary pointer-based data structures persistent. Eventually, we’ll reveal a general way to do this with \(O(1)\) additional space and \(O(1)\) slowdown, first published by Sleator and Tarjan et al. We’re mainly going to discuss partial persistence to make the explanation simpler, but their paper achieves full persistence as well.
First try: fat nodes
One natural way to make a data structure persistent is to add a modification history to every node. Thus, each node knows what its value was at any previous point in time. (For a fully persistent structure, each node would hold a version tree, not just a version history.)
This simple technique requires \(O(1)\) space for every modification: we just need to store the new data. Likewise, each modification takes \(O(1)\) additional time to store the modification at the end of the modification history. (This is an amortized time bound, assuming we store the modification history in a growable array. A fully persistent data structure would add \(O(\log m)\) time to every modification, since the version history would have to be kept in a tree of some kind.)
Unfortunately, accesses have bad time behavior. We must find the right version at each node as we traverse the structure, and this takes time. If we’ve made \(m\) modifications, then each access operation has \(O(\log m)\) slowdown, and a query in our region computation will take \(O(\log^2 n)\) time: not so great. (In a partially persistent structure, a version is uniquely identified by a timestamp. Since we’ve arranged the modifications by increasing time, you can find the right version by binary search on the modification history, using the timestamp as key. So it takes \(O(\log m)\) time to find the last modification before an arbitrary timestamp. The time bound is the same for a fully persistent structure, but a tree lookup is required instead of a binary search.)
Second try: path copying
Another simple idea is to make a copy of any node before changing it. Then you have to cascade the change back through the data structure: all nodes that pointed to the old node must be modified to point to the new node instead. These modifications cause more cascading changes, and so on, until you reach a node that nobody else points to—namely, the root. (The cascading changes will always reach the root.) Maintain an array of roots indexed by timestamp; the data structure pointed to by time \(t\)’s root is exactly time \(t\)’s data structure. (Some care is required if the structure can contain cycles, but it doesn’t change any time bounds.) (Random note: this happens to be the data model for the repository in the Subversion version control system.)
Figure 2 shows an example of path copying on a binary search tree. Making a modification creates a new root, but we keep the old root around for later use; it’s shown in dark grey. Note that the old and new trees share some structure (light grey nodes).
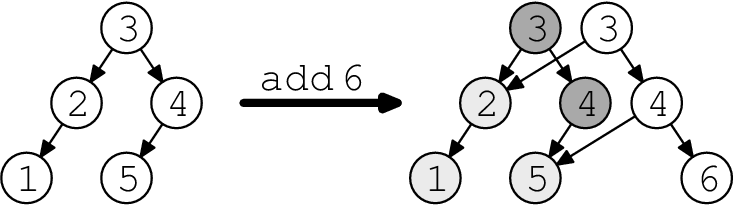
Access time does better on this data structure. Accesses are free, except that you must find the correct root. With \(m\) modifications, this costs \(O(\log m)\) additive lookup time—much better than fat nodes’ multiplicative \(O(\log m)\) slowdown, and lets us keep the \(O(\log n)\) query time in our region application.
Unfortunately, modification time and space is much worse. In fact, it’s bounded by the size of the structure, since a single modification may cause the entire structure to be copied. That’s \(O(m)\) for one update, and thus \(O(n^2)\) preprocessing time in the region application.
Path copying applies just as well to fully persistent data structures.
Sleator, Tarjan et al.
Sleator, Tarjan et al. came up with a way to combine the advantages of fat nodes and path copying, getting \(O(\log m)\) access time and \(O(1)\) modification space and time. Here’s how they did it, in the special case of trees.
In each node, we store one modification box. This box can hold one modification to the node—either a modification to one of the pointers, or to the node’s key, or to some other piece of node-specific data—and a timestamp for when that modification was applied. Initially, every node’s modification box is empty. We can think of this as being a very short log with at most one entry.
Whenever we access a node, we check the modification box, and compare
its timestamp against the access time. (The access time specifies the
version of the data structure that we care about.) If the modification
box is empty, or the access time is before the modification
time, then we ignore the modification box and just deal with the normal
part of the node. On the other hand, if the access time is
after the modification time, then we use the value in the
modification box, overriding that value in the node. (Say the
modification box has a new left pointer. Then we’ll use it
instead of the normal left pointer, but we’ll still use the
normal right pointer.)
Modifying a node works like this. (We assume that each modification touches one pointer or similar field.) If the node’s modification box is empty, then we fill it with the modification. Otherwise, the modification box is full. We make a copy of the node, but using only the latest values. (That is, we overwrite one of the node’s fields with the value that was stored in the modification box.) Then we perform the modification directly on the new node, without using the modification box. (We overwrite one of the new node’s fields, and its modification box stays empty.) Finally, we cascade this change to the node’s parent, just like path copying. (This may involve filling the parent’s modification box, or making a copy of the parent recursively. If the node has no parent—it’s the root—we add the new root to a sorted array of roots.)
Figure 3 shows how this works on a persistent search tree. The modification boxes are shown in grey.
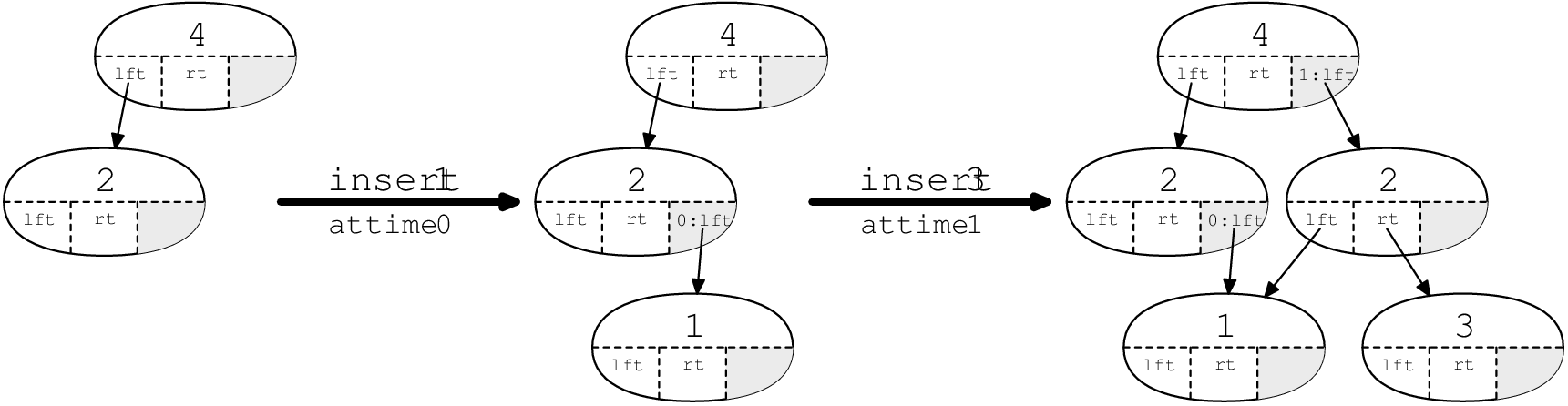
With this algorithm, given any time \(t\), at most one modification box exists in the data structure with time \(t\). Thus, a modification at time \(t\) splits the tree into three parts: one part contains the data from before time \(t\), one part contains the data from after time \(t\), and one part was unaffected by the modification.

How about time bounds? Well, access time gets an \(O(1)\) slowdown (plus an additive \(O(\log m)\) cost for finding the correct root), just as we’d hoped! (We must check the modification box on each node we access, but that’s it.)
Time and space for modifications require amortized analysis. A modification takes \(O(1)\) amortized space, and \(O(1)\) amortized time. To see why, use a potential function \(\Phi\), where \(\Phi(T)\) is the number of full live nodes in \(T\). (We can remember this as “fat children have potential”.) The live nodes of \(T\) are just the nodes that are reachable from the current root at the current time (that is, after the last modification). The full live nodes are the live nodes whose modification boxes are full.
So, how much does a modification cost? Each modification involves some number of copies, say \(k\), followed by 1 change to a modification box. (Well, not quite—you could add a new root—but that doesn’t change the argument.) Consider each of the \(k\) copies. Each costs \(O(1)\) space and time, but decreases the potential function by one! (Why? First, the node we copy must be full and live, so it contributes to the potential function. The potential function will only drop, however, if the old node isn’t reachable in the new tree. But we know it isn’t reachable in the new tree—the next step in the algorithm will be to modify the node’s parent to point at the copy! Finally, we know the copy’s modification box is empty. Thus, we’ve replaced a full live node with an empty live node, and \(\Phi\) goes down by one.) The final step fills a modification box, which costs \(O(1)\) time and increases \(\Phi\) by one.
Putting it all together, the change in \(\Phi\) is \(\Delta\Phi = 1 - k\). Thus, we’ve paid \(O(k + \Delta\Phi) = O(1)\) space and \(O(k + \Delta\Phi + 1) = O(1)\) time!
What about non-tree data structures? Well, they may require more than one modification box. The limiting factor is the in-degree of a node: how many other nodes can point at it. If the in-degree of a node is \(k\), then we must use \(k\) extra modification boxes to get \(O(1)\) space and time cost.
The geometric search problem
Let’s return to the geometric search problem discussed in Section 1. We now know how to make a persistent tree; but what kind of balanced tree should we use?
It turns out that this is one application where splay trees crash and burn. The reason is splaying. Every rotation while we access a splay tree is a modification, so we do \(O(\log n)\) modifications (costing an additional \(O(\log n)\) space) per access—including reads!
A less sexy balanced tree, like a red-black tree, is a better choice. Red-black trees keep themselves balanced with at most one rotation per modification (and a bunch of fiddling with red/black bits). This looks good—accesses are cheaper, and modifications cost \(O(1)\)—almost. The “almost” is because of red/black bit fiddling, which may affect a lot more than one node on the tree. A fully persistent red-black tree would need to keep the proper values for the red/black bits for every single version of the tree (so that further modifications could be made). This would mean that changing a red/black bit would count as a modification, and would have a persistence-related cost. Luckily, in the geometric search problem, we won’t need to look at the red/black bits when doing lookup on old versions of the tree: we only use them during the preprocessing when building the tree, and we only ever care about their newest value. So we don’t do any logging on the red-black bits: we’ll only log and copy when we change actual pointers. So only a constant number of logged changes happen in each operation, so we pay \(O(1)\) persistence-related cost per modification.